
Le piccole distanze sulla terra che noi usiamo quotidianamente possono presumere che la terra sia piatta. Ma questa presunzione può portare a errori.
La geometria più classica che c'è
Già dai primi anni di liceo, in geometria, si studiano i cinque postulati di Euclide:
- Per due punti distinti del piano passa una e una sola retta;
- Una linea retta può essere prolungata indefinitamente;
- Dato un punto e una lunghezza si può descrivere una circonferenza;
- Tutti gli angoli retti sono congruenti;
- Se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, prolungando indefinitamente le due rette, esse si incontreranno dalla parte dove la somma dei due angoli coniugati interni è minore di due angoli retti.
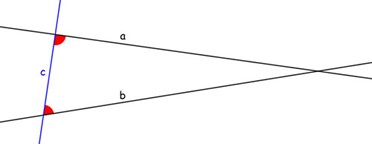
Il quinto postulato: necessario?
Vista la lunghezza del quinto postulato, ci verrebbe da pensare che sia dimostrato. Invece è un assioma come gli altri quattro!
Il bello dei sistemi assiomatici è che si possono modificare o cambiare, pervenendo a una “matematica diversa”. Questo hanno fatto in molti a partire dal 1833, quando il matematico transilvano János Bolyai dimostrò, basandosi sulle ricerche iniziate dal padre Farkas, l’indipendenza del quinto postulato, che quindi era stato posto da Euclide come assioma*.
Che un postulato sia indipendente da un sistema significa che facendo uso di detto sistema non è possibile implicare il postulato o il suo contrario.
Bolyai non si fermò, e teorizzò una geometria iperbolica dove la somma degli angoli interni di un triangolo non coincidesse con un angolo piatto. Ne uscì fuori che non solo le rette sono curve, ma anche che, dati una retta e un punto, si può tracciare una sola parallela.
* Nonostante Bolyai avesse avuto un ruolo non irrilevante nel dimostrare l’esistenza della geometria non euclidea, il primo ad averlo fatto sarebbe stato il russo Nikolaj Ivanovič Lobačevskij nel 1829. Bolyai però accelerò la diffusione della scoperta, essendo ai tempi più facile diffondere in Europa le pubblicazioni edite in Transilvania, piuttosto che le teorie scoperte a Kazan, dove Lobačevskij operava e occupava la carica di rettore dell’Università.

La geometria della terra
Un’altra forma di geometria più tangibile alla nostra esperienza è la geometria sferica.
Pensiamo per esempio a come tracciamo le distanze tra i punti della terra (che viene spesso e volentieri approssimata dai matematici a una sfera perfetta): se si considerano due meridiani e un parallelo, quest’ultimo incrocia i meridiani ad angoli retti, ma sebbene la somma dei coniugati sia un angolo piatto, i meridiani si incontrano ai poli. Possiamo osservare, quindi, come ciò violi il V postulato di Euclide. Non solo, queste rette altro non sono che le circonferenze aventi come centro quello della nostra sfera (le geodetiche) e si può dimostrare che non esistono due rette parallele.
Il problema virale
La geometria sferica è, inoltre, la chiave per risolvere il seguente problema virale:
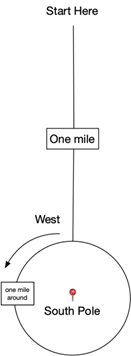
“Cammino di un miglio a Sud, uno a Ovest e uno a Nord. Finisco dove sono partito. Dove sono?”
Una soluzione banale al quesito è affermare che il narratore si trovi al polo Nord, dal momento che muovendosi verso ovest o verso est camminerebbe lungo una circonferenza avente come centro il polo. Ma un’altra soluzione non banale è che il narratore stia a un miglio a nord rispetto alla circonferenza lunga 1/n miglia avente come centro il polo Sud, corrispondente quest’ultimo a n naturale. Infatti, percorrendo il miglio a sud il personaggio andrebbe verso la circonferenza, proseguendo con il miglio a ovest compirebbe n giri di circonferenza con i quali annullerebbe questa stessa mossa. Il miglio a nord, infine, lo riporterebbe al punto di partenza. In una geometria euclidea, per esempio quella cartesiana, il problema sarebbe irrisolvibile perché il personaggio concluderebbe il percorso sempre un miglio a ovest rispetto al punto di partenza.
Un’ultima curiosità: la geometria sferica si inserisce all’interno della geometria ellittica di Bernhard Riemann. Quest’ultima ha la proprietà per cui la somma degli angoli interni di un triangolo eccede l’angolo piatto.


Dario Sanfilippo, Redazione SSC UniCT
"Sono sicuro che è più facile imparare la matematica che non il baseball." Albert Einstein al giocatore di baseball Moe Berg, ante 1941
E dunque la Scuola Superiore di Catania?
La formazione d’eccellenza è uno degli asset principali della Scuola Superiore di Catania. Gli allievi, in parallelo alle lezioni all’università, seguono in loco i corsi specialistici, che si distinguono per qualità e prestigio, tenuti anche da personalità internazionali e adattati ai propri interessi di ricerca, per avvicinarli precocemente a essa.
Opportunità
Il tutor è un professore o ricercatore dell’Università di Catania o di un’istituzione con essa convenzionata che segue individualmente ciascun allievo.
È scelto da ciascun allievo in funzione di cosa vuole approfondire per le sue future attività di ricerca. È compito del tutor fornire un approccio metodico alla ricerca stessa, erogando egli stesso o facendo erogare da personalità contattate i corsi specialistici. #UnlockMath
Vuoi saperne di più?




