
Facciamo un gioco: si scelga un qualsiasi numero naturale. Se è pari, lo si dimezzi, se è dispari, lo si triplichi e si aggiunga 1. Ripetere. Se per esempio scelgo 10, ottengo iterando ogni volta 5, 16, 8, 4, 2, 1.
Una congettura ostica
Ma si arriva a 1 con tutti i numeri? Questo è uno dei problemi aperti della matematica, la cosiddetta congettura di Collatz. Formulata nel 1937 dal matematico tedesco Lothar Collatz, ha affascinato molti studiosi della teoria dei numeri a causa del suo stato di problema irrisolto nonostante la sua semplice impostazione.
Finora non si è trovato nessun numero che violi la regola che si arriva fino a 1 con sufficienti iterazioni, e parliamo di numeri di 21 cifre al massimo.
Non esiste nessuna dimostrazione per o contro la tesi data (cioè che 1 è sempre il risultato finale), infatti i matematici hanno da sempre cercato metodi per trovare controesempi.
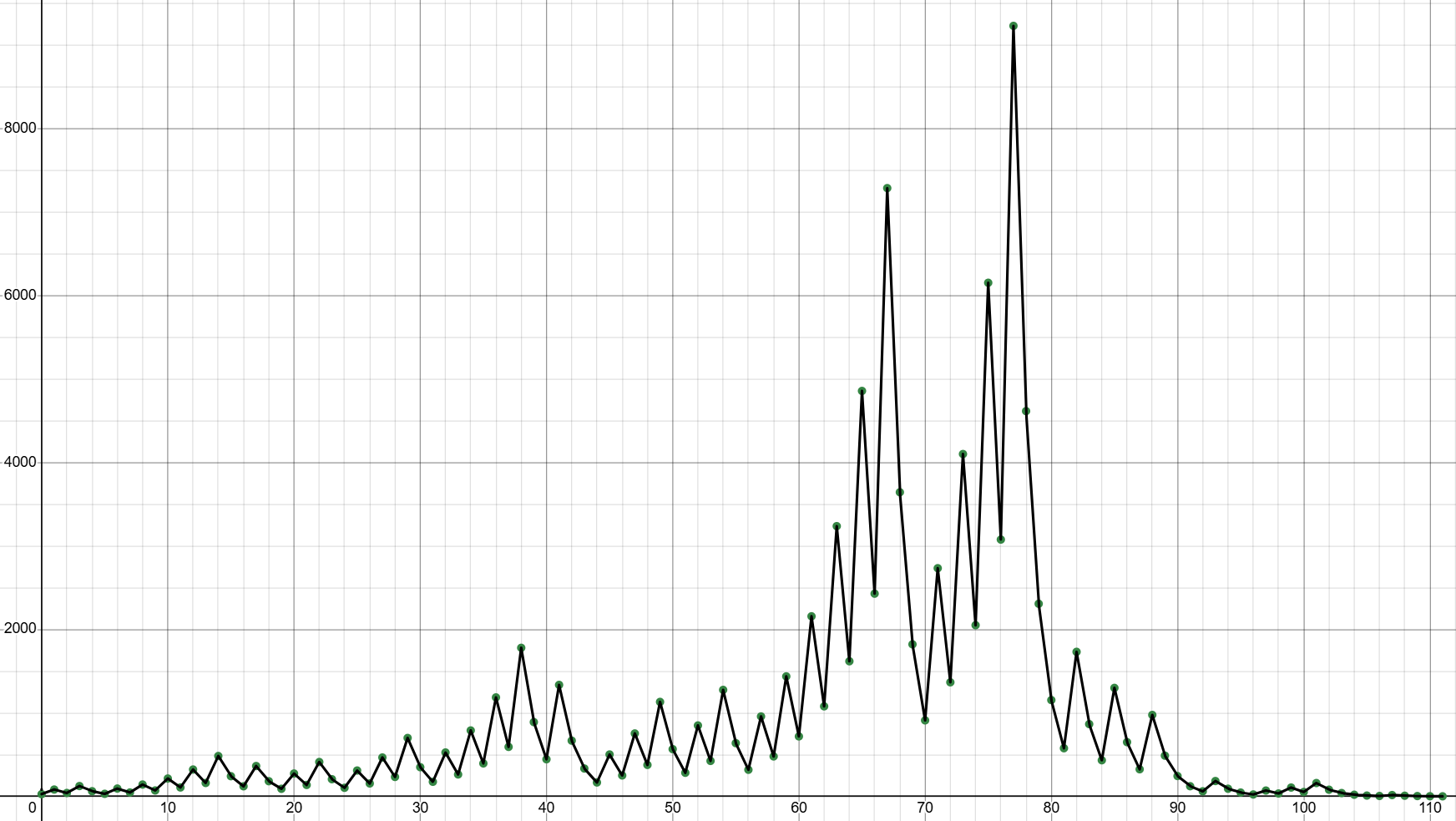
Sfidando la gravità
Il primo è di considerare, iterazione per iterazione, il “percorso” fatto dal numero: su un piano cartesiano si segna il punto (0, n0) con n0 il numero da analizzare, poi (1, n1) con n1 il risultato dalla prima iterazione, poi (2, n2) con n2 il numero dopo la seconda iterazione, e via dicendo fino a quando l’ordinata raggiunge 1. Per motivi grafici si congiungono i punti come in un gioco di enigmistica. Il diagramma ottenuto è detto dei numeri viandanti di n0, e la ricerca del controesempio si focalizza a cercare una sequenza viandante che, anziché scendere, sale. Il problema è che per salire, il numero deve essere dispari, e dopo l’iterazione si ottiene sempre un numero pari, perché dispari*dispari=dispari e dispari+dispari=pari. Sarà allora necessario trovare un numero pari che è il risultato dell’operazione 3n+1 con n dispari e che se dimezzato si ottiene un numero dispari per salire ancora. Il problema si ripete andando avanti nelle iterazioni, e risolverlo diventa sempre più complesso.
Alla ricerca dei cicli
Una seconda strategia consiste nel trovare dei cicli non banali, cioè dei numeri che si ripetono nella sequenza dei numeri viandanti oltre il classico ciclo 4-2-1. Si è però dimostrato che la lunghezza di questo ciclo è di almeno 186 miliardi di termini, che diventano più di 355 miliardi se non fosse coinvolto nessun numero al di sotto del 3*269. Si sa inoltre che il numero di termini è un numero ottenuto moltiplicando per tre numeri naturali tre numeri specifici nelle decine di milioni.
L'albero di Collatz
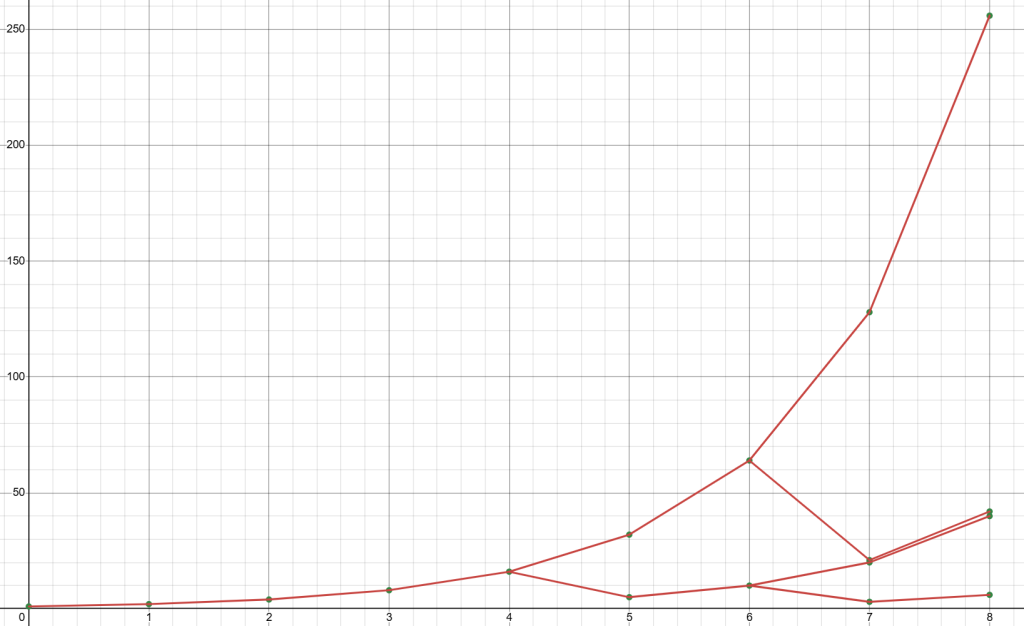
Al di fuori delle tentate dimostrazioni, è interessante notare come l’impostazione è equivalente a chiedersi se tutti i numeri compaiono in un albero, dove ogni numero è collegato al suo doppio e, se congrui a 4 modulo 6, a un terzo del numero meno 1. L’albero di Collatz comincia con pochi numeri in ciascuna iterazione, ma poi ramifica rapidamente. Qui è stato disegnato per le prime 8 iterazioni, quindi raffigura i numeri che portano a 1 entro 8 iterazioni comprese e quante iterazioni ci vogliono.
Se volete mettervi a risolvere la congettura di Collatz, e se la risolveste, vincereste un bando del Clay Institute of Mathematics per un premio da un milione di dollari. Non sareste però i primi a vincerlo, il primo è stato Grigorij Jakovlevič Perel’man che risolse la congettura di Poincaré, ma rifiutò il milione e ogni altro premio assegnatogli per questa sua scoperta. Se volete il milione in un altro modo, dovreste risolvere uno degli altri cinque problemi aperti nel bando del Clay Institute.


Dario Sanfilippo, Redazione SSC UniCT
"Sono sicuro che è più facile imparare la matematica che non il baseball." Albert Einstein al giocatore di baseball Moe Berg, ante 1941
E dunque la Scuola Superiore di Catania?
La formazione d’eccellenza è uno degli asset principali della Scuola Superiore di Catania. Gli allievi, in parallelo alle lezioni all’università, seguono in loco i corsi specialistici, che si distinguono per qualità e prestigio, tenuti anche da personalità internazionali e adattati ai propri interessi di ricerca, per avvicinarli precocemente a essa.
Opportunità
Il tutor è un professore o ricercatore dell’Università di Catania o di un’istituzione con essa convenzionata che segue individualmente ciascun allievo.
È scelto da ciascun allievo in funzione di cosa vuole approfondire per le sue future attività di ricerca. È compito del tutor fornire un approccio metodico alla ricerca stessa, erogando egli stesso o facendo erogare da personalità contattate i corsi specialistici. #UnlockMath
Vuoi saperne di più?




